Convergencia y límite
Se dice que un número real l es límite de una sucesión {a
n} y se denota:
Se dice que la sucesión {
a n} tiene límite +∞ y se denota:
Se dice que la sucesión {a n} tiene límite -∞ y se denota:
Sucesiones monótonas

Sucesiones estrictamente crecientes
Se dice que una sucesión es estrictamente creciente si cada término es mayor que el anterior.
an+1 > an
2, 5, 8, 11, 14, 17,...
5 > 2; 8 > 5; 11 > 8; ...
Sucesiones crecientes
Se dice que una sucesión es creciente si cada término es mayor o igual que el anterior.
an+1 ≥ an
2, 2 , 4, 4, 8, 8,...
2 ≥ 2; 4 ≥ 2; 4 ≥ 4; ...
Sucesiones estrictamente decrecientes
Se dice que una sucesión es estrictamente decreciente si cada término de la sucesión es menor que el anterior.
an+1 < an
1, 1/2, 1/3, 1/4, 1/5, 1/6,...
1/2 < 1; 1/3 < 1/2 ; 1/4 < 1/3; ...
Sucesiones decrecientes
Se dice que una sucesión es decreciente si cada término de la sucesión es menor o igual que el anterior.
Es monotona estrictamente decreciente.
an+1 ≤ an

3, 4/3, 1, 6/7,...
La sucesión va decreciendo.




Es monotona estrictamente decreciente.
2.-

2, − 4, 8, − 16, ...
No es monótona.
3.-
No es monótona.

No es monótona.
Sumas y notación Sigma
La sumatoria o sumatorio (llamada también notación sigma ) es una operación matemática que se emplea para calcular la suma de muchos o infinitos sumandos.
La operación sumatoria se expresa con la letra griega sigma mayúscula Σ, y se representa así:

Expresión que se lee: " sumatoria de Xi, donde i toma los valores desde 1 hasta n ".
x es la variable
i es el valor inicial, llamado límite inferior.
n es el valor final, llamado límite superior.
Pero necesariamente debe cumplirse que:
i ≤ n
Si la sumatoria abarca la totalidad de los valores, entonces no se anotan sus límites y su expresión se puede simplificar:Si la sumatoria abarca la totalidad de los valores, entonces no se anotan sus límites y su expresión se puede simplificar:
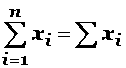
EJEMPLO
Si se quiere expresar la suma de los cinco primeros números naturales se puede hacer de esta forma:
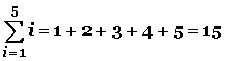
BIBLIOGRAFIA


Comentarios
Publicar un comentario